It's common in coding to face problems that require searching a graph. And there are different ways to search a graph depending on the requirements and the type of graph.

What is a graph?

A graph is a set of elements that are related. We call the elements nodes or vertices, and the connections edges. Sometimes the edges can carry information about the relation of the vertices, we call those weights.

Here are some examples of how different graphs can be visualized:

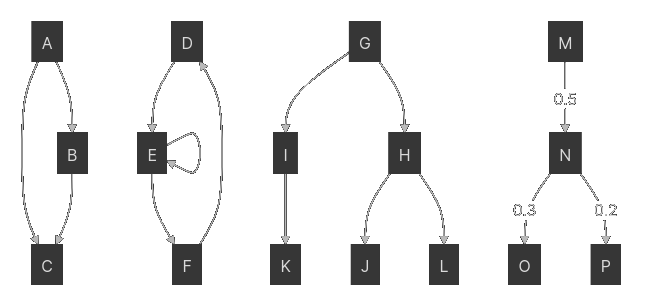
What kinds of graphs there are?

This is a big topic, so we won't go into too much depth, but I'll name the main traits that a graph can have to give some context.

A graph can be directed or undirected, meaning that the edges may have a sense or direction or not. On the examples above, we can see vertices connected by lines that have arrows in one side. That means there is only one direction that the relation can travel from one vertex to the other. All those graphs are directed.

A graph can be weighted or unweighted, meaning that the edges connecting the vertices carry a weight indicating the relation value between those vertices. Depending on the purpose of the graph that weight can mean different things, but generally it can be understood as the cost of crossing the edge.

A graph can be cyclic or acyclic. A cyclic graph will contain loops between some of its vertices, and that is relevant when applying algorithms that run over the graph, because depending on how the algorithm deals with that, it could get stuck. Therefore, whether a graph is cyclic or not is an important property of it.

Now that we have refreshed some concepts...

How we can search a graph?

Depending on which kind of search we want to do, we can use some algorithms or others.

For instance, if we want to find the path that connects two vertices in an unweighted graph, there are a couple of algorithms that are commonly used.

Those are DFS or Depth-First Search, and BFS or Breadth-First Search.

These two do not take into account the weights on the graph, so they are not the best candidates to find the shortest path between two vertices when the weights connecting them are important to us. They can be used for such a task, but it's not performant because the way they do so is to run across the whole graph, only to afterwards check the computed cost of each path.

Lets deep a bit on these two different algorithms, so we can understand their differences.

Breadth-First Search (BFS)

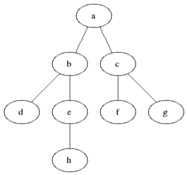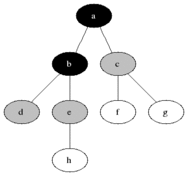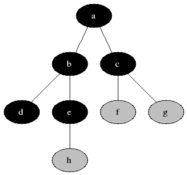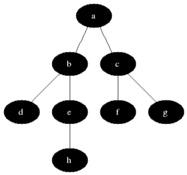
BFS is an algorithm that can be used to traverse any connected graph. It does so by starting on the root node, and then checking every connected node on the current depth level before going one level deeper.

Depth-First Search (DFS)

DFS is an algorithm that can also be used to traverse any connected graph. It does so by starting on the root node, and then exploring a branch until the end by going deeper. When the branch reaches the end, the algorithm backtracks up and starts on the next possible branch.

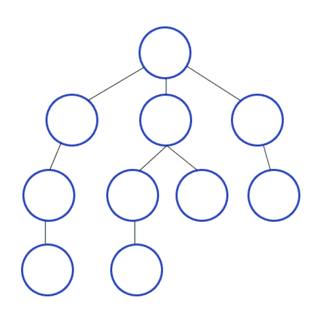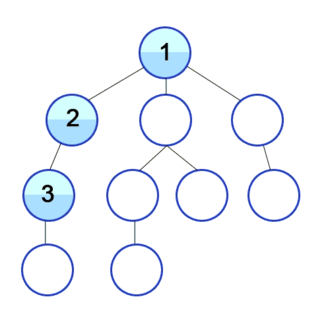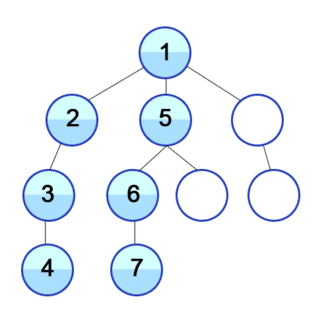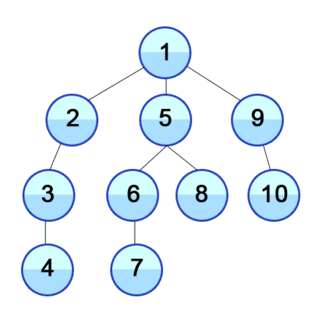
BFS vs DFS

Broadly speaking, the conceptual difference between those two algorithms is that BFS will check in rows, while DFS will check in columns. Another way of seeing it is that, BFS will check all its siblings before moving to the next children, whereas DFS will check all its children before moving to its sibling.

DFS is commonly implemented with recursion, whereas BFS is not. Not because it's not possible, but because there is a clear overhead in doing so.

But if we remove recursion from the equation, one pragmatic way to differentiate those two algorithms would be:

• BFS is normally implemented using a queue
• DFS is normally implemented using a stack

The data structure that we use to store the next elements will influence the way we consume them.

A queue is a FIFO(first-in first-out) structure, the next elements to be processed will be the added first, therefore we will completely check a level before going a level another level deep.

In contrast, a stack is a LIFO(last-in first-out) structure, the next elements to be processed will be the lasts that were added, therefore the algorithm will go deep first, and only when it runs out of depth will continue on the top level elements.

DFS has a risk versus BFS, and it is that it could get trapped in a infinity branch if that could exist, and would never finish execution. Whereas BFS would check the whole graph before getting trapped.

Other algorithms for weighted graphs

In the case that our graph is weighted, we have more options to execute a more performant search of a path, or paths, connecting two different nodes.

I won't discuss them in depth, but will name the more known here to have a good overview of the options.

• Dijkstra's algorithm: It's an algorithm that finds the shortest path between a starting node and all other nodes in a weighted graph. It uses a priority queue to explore the graph and guarantees finding the shortest path.

• A* algorithm: Another algorithm that finds the shortest path between a starting node and a target node in a weighted graph. It uses a heuristic function to guide the search towards the target node and can be more efficient than Dijkstra's algorithm.

• Bellman-Ford algorithm: Another algorithm that finds the shortest path between a starting node and all other nodes in a weighted graph that may contain negative edge weights. It can handle graphs with negative cycles, but is slower than Dijkstra's algorithm.

Conclusion

Graphs are something that is commonly encountered in programming and problem-solving, and searching a graph is a very common task.

There are different ways to search a graph depending on the constraints that we have on out information, as also the requirements that we have for our solution.

Knowing some ways to search them is going to help to model a solution when we encounter a problem that requires processing this kind of data structure.

x